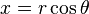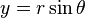Es un sistema de coordenadas bidimensional en el cual cada punto o posición del plano se determina por un angulo y una distancia.
Cualquier punto del plano corresponde a un par de coordenadas:
(r, θ)
en donde:
r = radio o distancia entre el punto y el origen de plano cartesiano tambien llamada coordenada radial
y
θ = es el angulo positivo en sentido antihorario tambien llamada coordenada angular
Definido un punto en coordenadas polares por su ángulo θ sobre el eje x, y su distancia r al centro de coordenadas, se tiene: